Project Euler: Problema 40 (python). 8e-05 segundos

El problema 40 de Project Euler dice lo siguiente:

An irrational decimal fraction is created by concatenating the positive integers:

0.123456789101112131415161718192021…

It can be seen that the 12^th digit of the fractional part is 1.

If d_n represents the n^th digit of the fractional part, find the value of the following expression.

d₁d₁₀d₁₀₀d₁₀₀₀d₁₀₀₀₀d₁₀₀₀₀₀d_1000000

Respuesta: 210

El problema trata de un número cuya parte decimal viene dada por la concatenación de los números (1, 2, 3, 4, 5, 6, …). Ahora bien, la primera idea que a uno se le viene a la mente es concatenar todos los números como si fuera strings, s = ‘0’ + '1’ + '2’ + '3’ + '4’ + '5’ + … hasta que la longitud de s, len(s), dé como resultado un número igual a 1000000. Luego simplemente multiplicamos “int(s[1]) * int(s[10]) * … int(s[1000000])” y eso sería la respuesta. Así es como lo hacen acá

http://alphacentauri32.wordpress.com/2011/05/04/project-euler-problem-40-solved-with-python/

Ello toma al rededor de 0.17 segundos en mi computadora. Sin embargo, me pregunté si había una manera más óptima de resolverlo. Entonces logré dar con una solución que es aproximadamente 1276 veces más rápido.

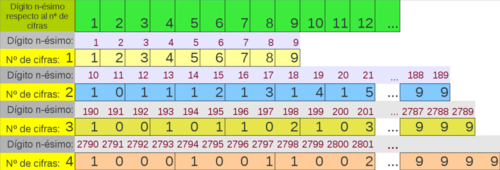
Sea 'dig’ el dígito 'n’-ésimo de la parte decimal del número 0.12345678910111213… Supongamos que queremos encontrar el dígito en la posición 2798. Según la imagen, nosotros sabemos que este  corresponde a un número de 4 cifras, el cual es 1002. Sabemos también que el mayor número de (4 - 1) cifras se sitúa en la posición 2789. Si restamos 2798 - 2789 obtenemos 9 dígitos restantes por contar, los cuáles se encuentran definitivamente en los números de 4 cifras. Finalmente, solo tenemos que contar 9 dígitos desde el primer número de 4 cifras, 1000. O lo que es lo mismo, hacer la división entera del número de dígitos resasntes entre el número de cifras (9 // 4 == 2) y sumarle 1, lo que da 3. Entonces, dígito se ubica en un número que es igual a 1000 + ( 3 - 1).

Obviamente, sin la imagen dada, nosotros no sabemos el número de cifras (n_cif) ni la posición que ocupa el dígito en el máximo número de (n_cif - 1). Todo esto lo hará el programa por nosotros. A diferencia de la solución del enlace, las iteraciones son mínimas. Lo siguiente es el código:

def dig_enesimo(n):
    n_cif = 0 #n corresponde a un numero de n_cif cifras
    suma = 0
    while suma < n:
        n_cif += 1
        digitos = 9 * n_cif * 10 ** (n_cif - 1) #{1cif->9 dig;2cif->180dig;3dig->2700dig...}
        suma += digitos
    suma = suma - digitos

    n_dig = n - suma #digitos restantes en un numero de n_cif cifras
    numero = n_dig // n_cif #contando de n_dig en n_dig
    pos_num = n_dig % n_cif #digitos sobrantes
    if pos_num != 0: numero += 1
    else: pos_num = n_cif
    pos_num = pos_num - 1 #dado un numero 'numero', pos_num es el digito en la posicion pos_num

    numero = 10 ** (n_cif - 1) + numero - 1
    dig = int(str(numero)[pos_num])
    
    return dig


result = 1
for i in [1, 10, 100, 1000, 10000, 100000, 1000000]:
    result *= dig_enesimo(i)

print result